马尔可夫决策过程

马尔可夫决策过程

  • Markov Decision Process, MDP

    提供了一套为在结果部分随机，部分在决策者的控制下的决策过程建模的数学框架

  • MDP 形式化地描述了一种强化学习环境

    • 环境完全可测（不用知道是之前是由怎么样来到当前状态的）
    • 当前状态可以完全表征过程（马尔可夫性质）

马尔可夫性质

The future is independent of the past given the present

定义

状态 StS_t 是马尔可夫的，当且仅当 P[St+1∣St]=P[St+1∣S1,...,St]\mathbb P[S_{t+1}|S_t]=\mathbb P[S_{t+1}|S_1,...,S_t]。

（St=f(Ht)S_t=f(H_t)）

性质

  • 状态从历史中捕获到了所有相关信息
  • 当状态已知的时候，可以抛开历史不管
  • i.e. 当前状态是未来的充分统计量

MDP 五元组

MDP可以由一个五元组表示：(S,A,{Psa},γ,R)(S,A,\{P_{sa}\},\gamma,R)

  • SS 是状态的集合。比如：迷宫中的为止，Atari 游戏中的当前屏幕显示

  • AA 是动作的集合。比如：像上下左右四个方向移动，手柄操纵杆的方向和按钮

  • PsaP_{sa} 是状态转移概率。

    • 对每个状态 s∈Ss\in S 和动作 a∈Aa\in A，PsaP_{sa} 是下一个状态在 SS 中的概率分布

      i.e. PsaP_{sa} 是映射到概率分布 Ω(S)\Omega(S) 中（可看作一个函数）

  • γ∈[0,1]\gamma\in[0,1] 是对未来奖励的折扣因子

  • R:S×A↔RR:S\times A\leftrightarrow \mathbb R 是奖励函数。有时奖励只与状态相关

MDP 的动态

MDP 的动态如下表示：

  • 从状态 s0s_0 开始
  • 智能体选择某个动作 a0∈Aa_0\in A
  • 智能体得到奖励 R(s0,a0)R(s_0,a_0)
  • MDP 随机转移到下一个状态 s1∼Ps0a0s_1\sim P_{s_0a_0}

这个过程不断进行：s0→a0,R(s0,a0)s1→a1,R(s1,a1)a2→a2,R(s2,a2)s3⋯s_0\xrightarrow{a_0,R(s_0,a_0)}s_1\xrightarrow{a_1,R(s_1,a_1)}a_2\xrightarrow{a_2,R(s_2,a_2)}s_3\cdots

直到终止状态 STS_T 出现为止，或者无止尽地进行下去

智能体的总回报为：R(s0,a0)+γR(s1,a1)+γ2(s2,a2)+⋯R(s_0,a_0)+\gamma R(s_1,a_1)+\gamma^2(s_2,a_2)+\cdots

基于动态规划的强化学习

MDP 目标和策略

目标

选择能够最大化累积奖励期望的动作：E[R(s0)+γR(s1)+γ2R(s2)+⋯ ]\mathbb E[R(s_0)+\gamma R(s_1)+\gamma^2R(s_2)+\cdots]

（所有的这些奖励都可能是随机的，故此处采用期望）

  • γ∈[0,1]\gamma\in[0,1] 表示未来奖励的折扣因子，使得和未来奖励相比起来智能体更重视即时奖励

    （以金融为例，今天的￥1 比明天的￥1 更有价值）

策略

给定一个特定的策略：π(s):S→A\pi(s):S\rightarrow A，即在状态 ss 下采取动作 a=π(s)a=\pi(s)

给策略 π\pi 定义价值函数：Vπ(s)=E[R(s0)+γR(s1)+γ2R(s2)+⋯∣s0=s,π]V^\pi(s)=\mathbb E[R(s_0)+\gamma R(s_1)+\gamma^2R(s_2)+\cdots|s_0=s,\pi]，即给定其实状态和根据策略 π\pi 采取动作时的累积奖励期望

价值函数的 Bellman 等式

给策略 π\pi 定义价值函数公式中的 γR(s1)+γ2R(s2)+⋯\gamma R(s_1)+\gamma^2R(s_2)+\cdots 项可以写成 γVπ(s1)\gamma V^\pi(s_1)。

因此可以得到 Bellman 等式：Vπ(s)=R(s)+γ∑s′∈Spsπ(s)(s′)Vπ(s′)V^\pi(s)=R(s)+\gamma\sum\limits_{s'\in S}p_{s\pi(s)}(s')V^{\pi}(s')

  • R(s)R(s) 即时奖励
  • psπ(s′)p_{s\pi}(s') 状态转移概率
  • Vπ(s′)V^{\pi}(s') 下一个状态的价值

最优价值函数

  • 对于状态 ss 来说的最优价值函数是所有策略可获得的最大可能折扣奖励和

    V∗(s)=max⁡πVπ(s)V^*(s)=\max\limits_{\pi}V^\pi(s)

  • 最优价值函数的 Bellman 等式

    V∗(s)=R(s)+max⁡a∈Aγ∑s′∈Spsa(s′)V∗(s′)V^*(s)=R(s)+\max\limits_{a\in A}\gamma\sum\limits_{s'\in S}p_{sa}(s')V^*(s')

  • 最优策略

    π∗(s)=arg⁡max⁡a∈A∑s′∈Spsa(s′)V∗(s′)\pi^*(s)=\arg\max\limits_{a\in A}\sum\limits_{s'\in S}p_{sa}(s')V^*(s')

  • 对状态 ss 和策略 π\pi

    V∗(s)=Vπ∗(s)≥Vπ(s)V^*(s)=V^{\pi^*}(s)\ge V^\pi(s)

价值迭代和策略迭代

价值函数和策略相关

Vπ(s)=R(s)+γ∑s′∈Spsπ(s)(s′)Vπ(s′)V^\pi(s)=R(s)+\gamma\sum\limits_{s'\in S}p_{s\pi(s)}(s')V^{\pi}(s')

π(s)=arg⁡max⁡a∈A∑s′∈Spsa(s′)Vπ(s′)\pi(s)=\arg\max\limits_{a\in A}\sum\limits_{s'\in S}p_{sa}(s')V^\pi(s')

可以对最优价值函数和最优策略执行迭代更新

  • 价值迭代
  • 策略迭代

价值迭代

对于一个动作空间和状态空间有限（∣S∣<∞,∣A∣<∞|S|\lt\infty,|A|\lt\infty）的 MDP

价值迭代过程

  1. 对每个状态 ss，初始化 V(S)=0V(S)=0

  2. 重复一下过程直到收敛

    • 对每个状态，更新 V(s)=R(s)+max⁡a∈Aγ∑s′∈Spsa(s′)V(s′)V(s)=R(s)+\max\limits_{a\in A}\gamma\sum\limits_{s'\in S}p_{sa}(s')V(s')

    注意：以上计算中没有明确的策略

同步 vs. 异步价值迭代

同步的价值迭代会储存两份价值函数的拷贝

  1. 对 SS 中的所有状态 ss

    Vnew(s)←max⁡a∈A(R(s)+γ∑s′∈Spsa(s′)Vold(s′))V_{new}(s)\leftarrow\max\limits_{a\in A}(R(s)+\gamma\sum\limits_{s'\in S}p_{sa}(s')V_{old}(s'))

  2. 更新 Vold(s)←Vnew(s)V_{old}(s)\leftarrow V_{new}(s)

异步价值迭代值只储存一份价值函数

  • 对 SS 中的所有状态 ss：V(s)←max⁡a∈A(R(s)+γ∑s′∈Spsa(s′)V(s′))V(s)\leftarrow\max\limits_{a\in A}(R(s)+\gamma\sum\limits_{s'\in S}p_{sa}(s')V(s'))

策略迭代

对于一个动作空间和状态空间有限（∣S∣<∞,∣A∣<∞|S|\lt\infty,|A|\lt\infty）的 MDP

策略迭代过程

  1. 随机初始化策略 π\pi

  2. 重复一下过程直到收敛

    • 让 V←VπV\leftarrow V^\pi（特别耗时）
    • 对每个状态，更新 arg⁡max⁡a∈A∑s′∈Spsa(s′)V(s′)\arg\max\limits_{a\in A}\sum\limits_{s'\in S}p_{sa}(s')V(s')

    更新价值函数会很耗时

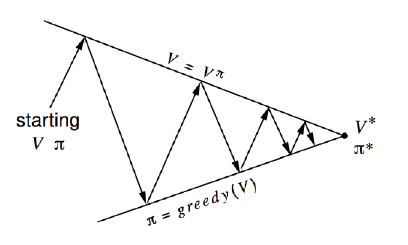
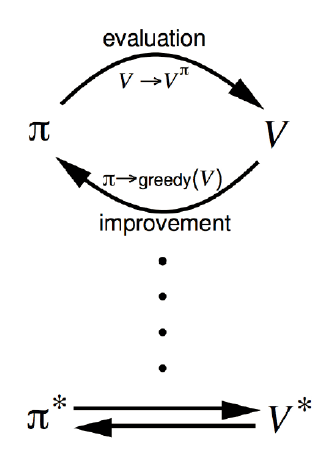
策略评估

  • 估计 VπV^\pi
  • 迭代的评估策略

策略改进

  • 生成 π′≥π\pi'\ge\pi
  • 贪心策略改进

总结

  1. 价值迭代是贪心更新法
  2. 策略迭代中，用 Bellman 等式更新价值函数的代价很大
  3. 对于空间较小的 MDP，策略迭代通常很快收敛
  4. 对于空间较大的 MDP，价值迭代更实用（效率更高）
  5. 如果没有状态转移循环，最好使用价值迭代

基于模型的强化学习

学习一个 MDP 模型

目前我们关注在给定一个已知 MDP 模型后（状态转移函数 Psa(s′)P_{sa}(s') 和奖励函数 R(s)R(s) 明确给定后）

  • 计算最优价值函数
  • 学习最优策略

但是，在实际问题中，状态转移和奖励函数一般不是明确给出的。

比如，我们只看到了一些 episodes（采样）：

  • Episode1: s0(1)→a0(1),R(s0)(1)s1(1)→a1(1),R(s1)(1)s2(1)⋯sT(1)s_0^{(1)}\xrightarrow{a_0^{(1)},R(s_0)^{(1)}}s_1^{(1)}\xrightarrow{a_1^{(1)},R(s_1)^{(1)}}s_2^{(1)}\cdots s_T^{(1)}

  • Episode2: s0(2)→a0(2),R(s0)(2)s1(2)→a1(2),R(s1)(2)s2(2)⋯sT(2)s_0^{(2)}\xrightarrow{a_0^{(2)},R(s_0)^{(2)}}s_1^{(2)}\xrightarrow{a_1^{(2)},R(s_1)^{(2)}}s_2^{(2)}\cdots s_T^{(2)}

从“经验”中学习一个 MDP 模型

  • 学习状态转移概率 Psa(s′)P_{sa}(s') = 在 ss 下采取动作 aa 并转移到 s′s' 的次数 ÷ 在 ss 下采取动作 aa 的总次数
  • 学习奖励函数 R(s)R(s)，也就是立即奖赏期望 R(s)=average[R(s)(i)]R(s)=average[R(s)^{(i)}]

另一种解决方式是不学习 MDP，直接从经验中学习价值函数和策略

  • 也就是模型无关（Model-free）的强化学习

学习模型 & 优化策略

算法思路

  1. 随机初始化策略 π\pi
  2. 重复以下过程直到收敛
    • 在 MDP 中执行 π\pi 进行一些测验
    • 使用 MDP 中的累积经验更新 PsaP_{sa} 和 RR 的估计
    • 利用 PsaP_{sa} 和 RR 的估计执行价值迭代，得到新的估计价值函数 VV
    • 根据 VV 更新策略为 π\pi 为贪心策略