A3C

Actor-Critic

演员采取动作使评论家满意
评论家学会准确估计演员策略所采取动作价值的值函数

A2C

Advantage Actor-Critic

通过减去一个基线函数来优化评论家的打分

更多信息指导：降低较差动作概率，提高较优动作概率
进一步降低方差

优势函数 $A^\pi(s,a)=Q^\pi(s,a)-V^\pi(s)$

A3C：异步 A2C 方法

Asynchronous Advantage Actor-Critic

异步：算法涉及并执行一组环境
优势：策略梯度的更行使用优势函数
动作评价

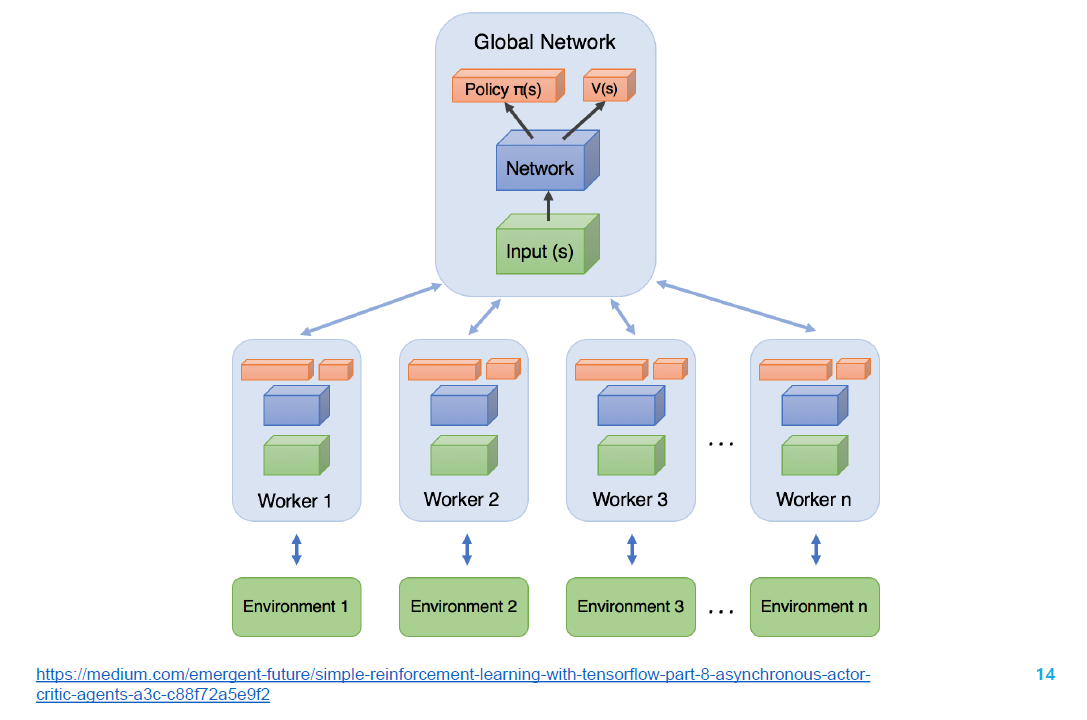
A3C 示意图

Global Network 是表演者和评论家的所在

这些 Workers 学习完一段时间后，产生梯度，传到 global network 中去。更新完全局网络后参数又同步到所有 workers 上去。这样的好处是并行化，提升性能。

A3C 算法伪代码

确定性策略梯度 DPG

随机策略与确定性策略

随机策略
- 对于离散动作： $\pi(a|s;\theta)=\frac{\exp\{Q_\theta(s,a)\}}{\Sigma_{a'}\exp\{Q_\theta(s,a')\}}$
- 对于连续动作： $\pi(a|s;\theta)\propto\exp\{(a-\mu_\theta(s))^2\}$
确定性策略
- 对于离散动作： $\pi(s;\theta)=\arg\max_aQ_\theta(s,a)$ 不可微
- 对于连续动作： $a=\pi(s;\theta)$ 可微

确定性策略梯度

用于估计状态-动作值的评论家模块

$Q^w(s,a)\simeq Q^\pi(s,a)$

$L(w)=\mathbb E_{s\sim\rho^\pi,a\sim\pi_\theta}[(Q^w(s,a)-Q^\pi(s,a))^2]$

确定性策略梯度定理

$J(\pi_\theta)=\mathbb E_{s\sim\rho^\pi}[Q^\pi(s,a)]$

$\nabla_\theta J(\pi_\theta)=\mathbb E_{s\sim\rho^\pi}[\nabla_\theta\pi_\theta(s)\nabla_a Q^\pi(s,a)|_{a=\pi_\theta(s)}]$

深度确定性梯度策略 DDPG

在 DPG 的基础上增加

经验重放（离线策略）
目标网络
在动作输入前对 Q 网络做 batch normalization
添加连续噪声

目标网络至关重要

信任区域策略优化 TRPO

策略梯度的缺点

步长难以确定：

采集到数据的分布会随策略的更新而变化
较差的步长产生的影响大，进而导致策略变差

TRPO

优化目标：策略梯度

第一种： $J(\theta)=\mathbb E_{\tau\sim p_\theta(\tau)}[\Sigma_t\gamma^tr(s_t,a_t)]$

第二种： $J(\theta)=\mathbb E_{s_0\sim p_\theta(s_0)}[V^{\pi_\theta}(s_0)]$

优化目标的优化量

$J(\theta')-J(\theta)=J(\theta')-\mathbb E_{s_0\sim p_\theta(s_0)}[V^{\pi_\theta}(s_0)]$

$=J(\theta')-\mathbb E_{\tau\sim p_{\theta'(\tau)}}[V^{\pi_\theta}(s_0)]$

$=J(\theta')-\mathbb E_{\tau\sim p_{\theta'(\tau)}}[\sum_{t=0}^\infty\gamma^tV^{\pi_\theta}(s_t)-\sum_{t=1}^\infty\gamma^tV^{\pi_\theta}(s_t)]$

$=J(\theta')+\mathbb E_{\tau\sim p_{\theta'(\tau)}}[\sum_{t=0}^\infty\gamma^t(\gamma V^{\pi_\theta}(s_{t+1})-V^{\pi_\theta}(s_t))]$

$=\mathbb E_{\tau\sim p_{\theta'(\tau)}}[\sum_{t=0}^\infty\gamma^tr(s_t,a_t)]+\mathbb E_{\tau\sim p_{\theta'(\tau)}}[\sum_{t=0}^\infty\gamma^t(\gamma V^{\pi_\theta}(s_{t+1})-V^{\pi_\theta}(s_t))]$

$=\mathbb E_{\tau\sim p_{\theta'(\tau)}}[\sum_{t=0}^\infty\gamma^t(r(s_t,a_t)+\gamma V^{\pi_\theta}(s_{t+1})-V^{\pi_\theta}(s_t))]$

$=\mathbb E_{\tau\sim p_{\theta'(\tau)}}[\sum_{t=0}^\infty\gamma^tA^{\pi_\theta}(s_t,a_t)]$

优势函数 $A^{\pi_\theta}(s_t,a_t)=Q^{\pi_\theta}(s_t,a_t)-V^{\pi_\theta}(s_t)$

使用重要性采样

$J(\theta')-J(\theta)$

$=\mathbb E_{\tau\sim p_{\theta'(\tau)}}[\sum_{t=0}^\infty\gamma^tA^{\pi_\theta}(s_t,a_t)]$

$=\sum_t\mathbb E_{s_t\sim p_{\theta'(s_t)}}[\mathbb E_{a_t\sim\pi_{\theta'}(a_t|s_t)}[\gamma^tA^{\pi_\theta}(s_t,a_t)]]$

$=\sum_t\mathbb E_{s_t\sim p_{\theta'(s_t)}}[\mathbb E_{a_t\sim\pi_{\theta'}(a_t|s_t)}[\frac{\pi_{\theta'}(a_t|s_t)}{\pi_\theta(a_t|s_t)}\gamma^tA^{\pi_\theta}(s_t,a_t)]]$