数字信号处理 六、时域数字信号处理之离散时间傅里叶变换

傅里叶论文：任何连续周期信号都可以由一组适当的正弦曲线组合而成

拉普拉斯赞成，拉格朗日反对

理论上，拉格朗日是对的；应用上，傅里叶是对的

为什么用正弦信号

正弦信号是周期的，分析容易。

正弦曲线的保真度，经过LTI后仍然是正余弦曲线

正余弦互为导数

基本思想

用对已知函数加权求和的方法表示出一个未知的函数。其中的权（系数），就是原函数影射至相应函数组的结果

对于需要研究的y[n]，定义$y[n]=\Sigma_{i}w_ix_i[n]$ 或者 $y(t)=∫_kw_kx_k(t)$

进而研究wi，其中wi是y[n]在xi[n]上的性质

此方法的好处

• y[n]中每个点都是独立的
• x[n]可用多种“工具盒”

傅里叶变换

傅里叶变换是最经典常见基础的变换方法

• 研究wi
• 研究xi[n]
• 研究y[n]

期末考点

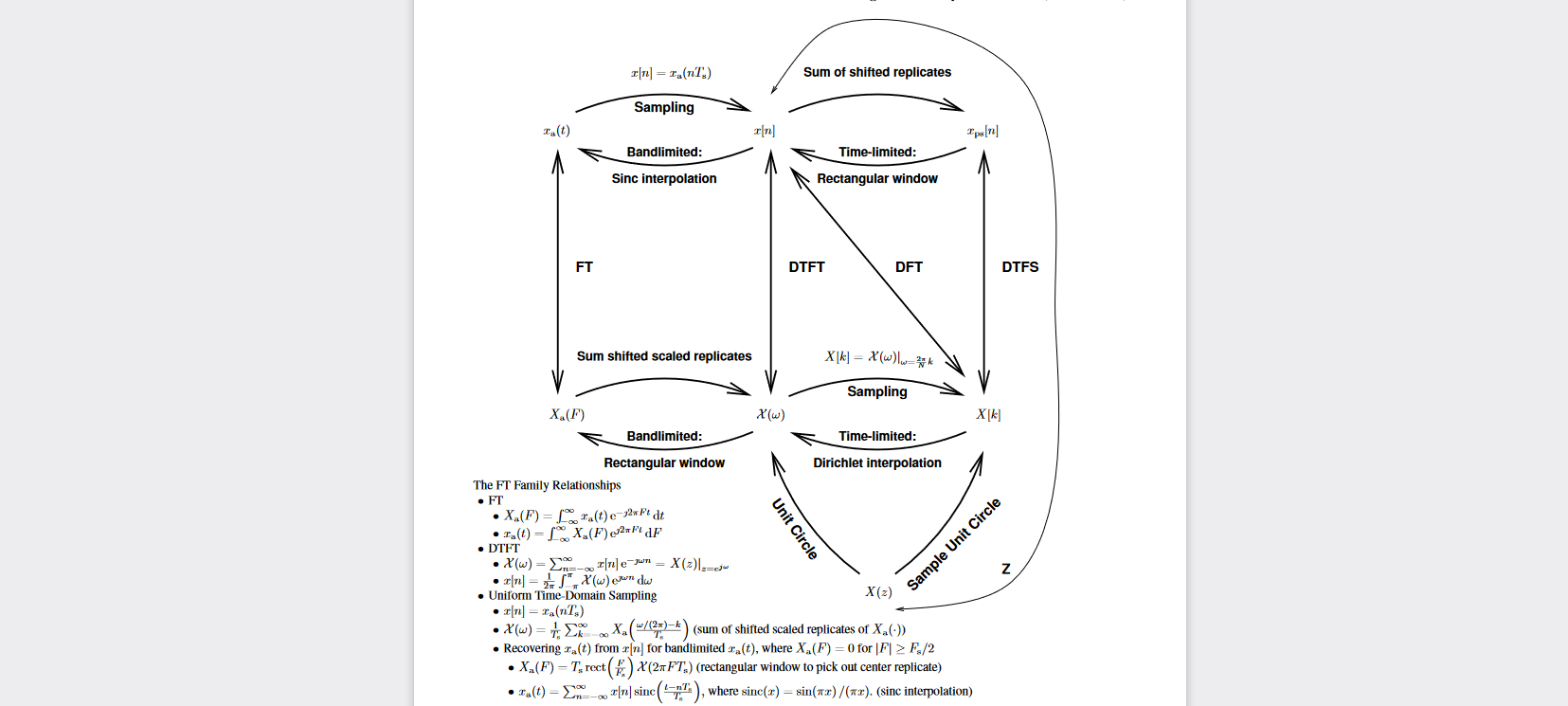
分类：傅里叶变换（非周期连续信号）、傅里叶级数（周期性连续信号）、离散时域傅里叶变换（非周期离散信号）、离散傅里叶变换（周期离散信号）

实数离散傅里叶变换

y[n]=C1向量×若干正弦信号+C2向量×若干余弦向量

问题：曲线有多少条？曲线是离散的还是连续的？C是什么？

朴素方法：一个序列的点个数N=曲线个数

取值范围wi 0到Π

如果信号和sin/cos曲线越像（相关性），权值越大

频谱的概念

由系数个数引发的重要概念→频域

将坐标系的

• 横轴定义为：第𝑘条曲线的序号𝑘

• 纵轴定义为：第𝑘条曲线的系数𝑤_𝑖 或𝑐_𝑖

此时我们发现横轴的意义是第𝑘条曲线，将其写成第𝑘条曲线对应的频率/角速度，而纵轴则是这个角速度/频率对应的正余弦曲线的权重系数，这个称之为信号的频谱

DFT的拓展

变换方法	处理对象
傅里叶变换 FT （Fourier Transform）	非周期、连续
傅里叶级数 FS （Fourier Series）	周期、连续
离散时间傅里叶变换DTFT	非周期、离散
离散傅里叶变换（级数）DFT(DFS)	周期、离散

时域的离散导致频域的周期

时域的连续导致频域的非周期

因为ω差2Π就会导致曲线一样。

时域的周期导致频域的离散

时域的非周期导致频域的连续

离散和周期是一对，连续和非周期是一对。

频域的离散代表有限条正余弦曲线，这些加起来必然是周期的

如果频域是连续的，说明有无线条曲线，这些曲线加起来就不是周期的

能量密度频谱

∫_{−∞}^∞|𝑥(𝑡)|^2𝑑𝑡=\frac{1}{2𝜋} ∫_{−∞}^∞|𝑋_𝑎(𝑗Ω)|^2𝑑Ω

上述关系通常被称为有限能量连续讯号的Parseval’s 关系式