阅读材料

课堂笔记

Convex Hull and Sorting

convex hull algorithms: $O(n\log n)$ .

can we do better?

convex hull of points is equivalent to sorted numbers.
$O(n\log n)$ worst-case is optimal.
fewer than n points on the hull
$O(n\log h)$ ?

Marriage Before Conquest

MbC(P:l,r): find Upper Hull of P from x-coordinates l to r

find median x-coordinate $x_m$ . partition into $P_l,P_r$ . $O(n)$ times
find the bridge, uv, over $x_m$ .
remove the points below the bridge. $O(n)$
recurse: $MbC(P_l:l,u_x)$ & $MbC(P_r:v_x,r)$ $f(\frac{n}{2})+f(\frac{n}{2})$

if step 2 can be done in linear time, the total time is $O(n\log h)$ .

How to find bridges

finding a bridge is equivalent to finding a line $Y=aX+b$ that:

passes above all the points
has the lowest intersection point with the separating line (the lowest point that is not inside the convex hull)

find $a$ and $b$ s.t.:

$y_i\le ax_i+b$ for every input point $(x_i,y_i)$
$y_m=ax_m+b$ is minimized

Linear Programming

unknowns: $x_1,\cdots,x_d$

minimize: $c_1x_1+c_2x_2+\cdots+c_dx_d$

s.t.

a_{1,1}x_1+a_{1,2}x_2+\cdots+a_{1,d}x_d\le b_1\\ a_{2,1}x_1+a_{2,2}x_2+\cdots+a_{2,d}x_d\le b_2\\ \cdots\cdots\\ a_{n,1}x_1+a_{n,2}x_2+\cdots+a_{n,d}x_d\le b_n\\

$\mathbf a$ , $\mathbf b$ , $\mathbf c$ are given as input.

$d$ dimensions

There a and b are unknown.

can be solved in $O(n)$ time on average.

1D Linear Programming

unknown $x_1$

minimize $c_1x_1$ s.t. $a_{i,1}x_1\le b_i$ for i in 1 to n

find feasible region

possible cases: feasible, infeasible or unbounded.

$O(n)$ running time

2D Linear Programming

unknown $x_1,x_2$

minimize $c_1x_1+c_2x_2$ s.t. $a_{i,1}x_1+a_{i,2}x_2\le b_i$ for i in 1 to n

假设一些直线找到了一个可行区域

现在就只需要平移 $c_1x_1+c_2x_2=V$ 这条直线，以找到最小值。

initialize $v$ .
for i=1 to n
1. if constraint i does not violate v: do nothing
2. else solve 1D Linear programming with constraints 1 to i-1 on boundary of constraint i

step 2.2 might run n times $O(n^2)$ time in total.

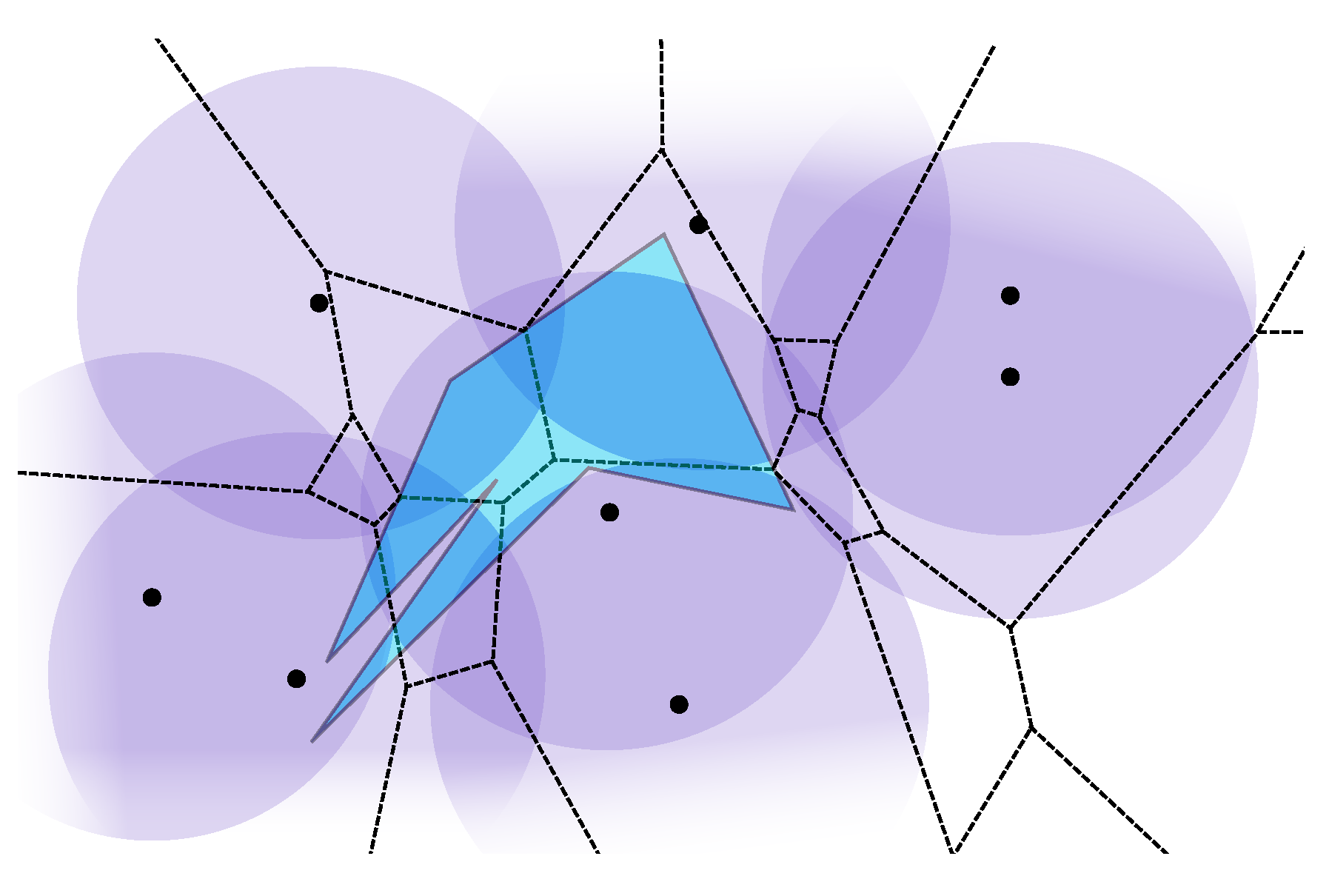
A randomized incremental algorithm

initialize v
randomly relabel (shuffle) constraints
for i = 1 to n
1. if constraint i does not violate v: do nothing
2. else solve 1D Linear Programming with constraints 1 to i-1 on boundary of constraint i
  意思就是新增的这个约束 i 对应的直线，把 x2 解出来，代入到前面 1 到 i-1 中的 x2，可以得到一个一维的线性规划问题。

improves from $O(n^2)%$ to $O(n)$ time on average.

backward analysis (a claim): the probability that step 3.2 runs during the i-th iteration of the for loop is $\le\frac{2}{i}$

expected running time:

\mathbb E[\sum_{i=1}^nRunning\ Time\ of\ i-th\ Iteration]\\ =\sum_{i=1}^n\mathbb E[Running\ Time\ of\ the\ i-th\ Iteration]\\ =\sum_{i=1}^n(\Pr[Step\ 3.2\ runs\ at\ the\ i-th\ Iteration]\cdot O(i)+O(1))\\ =\sum_{i=1}^n(\frac{2}{i}\cdot O(i)+O(1))=\sum_{i=1}^nO(1)\\ =O(n)

how to shuffle?

Place i in a random non-empty spot for i = 1 to n
fill i-th spot randomly for i = 1 to n
fill i-th spot randomly from i = n to 1

To proof the claim:

consider the step 3.2
every constraint is a line, we have n of them. $c_1,\cdots,c_n$ .
we have n positions in our shuffle.
the line is placed randomly in these n positions.
then the probability of entering 3.2:
Probability entering 3.2 at $i=n$ is: $\frac{2}{n}$ , because only two lines determin final result. since the order of lines are shuffled, the probability of n-th line is one of the two determin line is $\frac{2}{n}$ .
consider feasible region, the optimal solution is adjacent to 2 constraints $c_1,c_2$ . for i-th line probability would be $\frac{2}{i}$

Chan’s Algortihm

陈氏算法，计算凸包的一种快速算法，时间复杂度 $O(n\log h)$

预设一个凸包上的点的个数 $h\le2^{2^i}$ . $i$ 从 $1$ 开始尝试。

对每一个 i：

将当前所有点分成 $\frac{n}{h}$ 份，分别用 graham scan 计算凸包，这一步的时间复杂度为 $O(h\log h)$ 。计算 $\frac{n}{h}$ 次，所以总的时间复杂度为 $O(n\log h)$ 。
从这些凸包上 x 坐标最小的点开始，找到这 $\frac{n}{h}$ 个凸包合并的上凸包。就是对当前的点，找到通过分别二分查找 $O(\log h)$ 这 $\frac{n}{h}$ 个子凸包上和当前点连线正切值最小的点。这一步是 $O(\frac{n}{h}\log h)$ .
因为假设凸包点数的上界是 h，最多要找 h 次，所以找到这些子凸包的公共上凸包的总时间为 $O(n\log h)$
如果假设正确，那么整个算法的时间复杂度为 $O(n\log h)$ 。
如果算法错误，i++，并继续尝试计算。
假设最终凸包上的点数为 $h$ ，那么最多测试 $\log\log h$ 次。
所以总的时间复杂度为
$\sum_{i=1}^{\log\log h}O(n\log(2^{2^i}))\\ =\sum_{i=1}^{\log\log h}O(n2^i)=O(n2^{\log\log h})=O(n\log h)$